Ecliptic coordinate system

Not to be confused with Elliptic coordinates.

The ecliptic coordinate system is a celestial coordinate system that uses the ecliptic for its fundamental plane. The ecliptic is the path that the sun appears to follow across the celestial sphere over the course of a year. It is also the intersection of the Earth's orbital plane and the celestial sphere. The latitudinal angle is called the ecliptic latitude or celestial latitude (denoted β), measured positive towards the north. The longitudinal angle is called the ecliptic longitude or celestial longitude (denoted λ), measured eastwards from 0° to 360°. Like right ascension in the equatorial coordinate system, 0° ecliptic longitude is pointing towards the Sun from the Earth at the Northern hemisphere vernal equinox. This choice makes the coordinates of the fixed stars subject to shifts due to the precession, so that always a reference epoch should be specified. Usually epoch J2000.0 is taken, but the instantaneous equinox of the day (called the epoch of date) is possible too.

This coordinate system can be particularly useful for charting solar system objects. Most planets (except Mercury), and many small solar system bodies have orbits with small inclinations to the ecliptic plane, and therefore their ecliptic latitude β is always small. Because of the planets' small deviation from the plane of the ecliptic, ecliptic coordinates were used historically to compute their positions. (Aaboe 2001, 17-19)

Contents

Conversion between celestial coordinate systems

In the formulas below

Converting Cartesian vectors

Conversion from ecliptic coordinates to equatorial coordinates

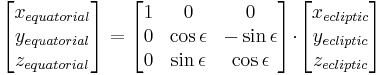
\begin{bmatrix} x_{equatorial} \\ y_{equatorial} \\ z_{equatorial} \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \epsilon & -\sin \epsilon \\ 0 & \sin \epsilon & \cos \epsilon \\ \end{bmatrix} \! \cdot \! \begin{bmatrix} x_{ecliptic} \\ y_{ecliptic} \\ z_{ecliptic} \\ \end{bmatrix}

(Seidelmann 1992, 555–8)

Conversion from equatorial coordinates to ecliptic coordinates

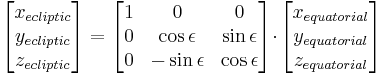
\begin{bmatrix} x_{ecliptic} \\ y_{ecliptic} \\ z_{ecliptic} \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \epsilon & \sin \epsilon \\ 0 & -\sin \epsilon & \cos \epsilon \\ \end{bmatrix} \! \cdot \! \begin{bmatrix} x_{equatorial} \\ y_{equatorial} \\ z_{equatorial} \\ \end{bmatrix}

(Seidelmann 1992, 555–8)

Converting angular quantities

Given ecliptic coordinates λ and β, the equatorial coordinates are:

α = atan2((sin λ cos ε - tan β sin ε), cos λ)
δ = asin(sin ε sin λ cos β + cos ε sin β)

Conversely, given equatorial coordinates α and δ, the ecliptic coordinates are:

λ = atan2((sin α cos ε + tan δ sin ε), cos α)
β = asin(sin δ cos ε - cos δ sin α sin ε)

(Jean Meeus: Astronomical Algorithms, 2nd Edition. ISBN 0-943396-61-1)

An algorithm

If the calculation is to be done with an electronic pocket calculator, it is best to use a rectangular to polar (R→P) and polar to rectangular (P→R) function, which are found on most scientific calculators. They avoid all the above problems and give us an extra sanity check as well.

The algorithm for the ecliptic to equatorial transformation then becomes:

Similarly for the equatorial to ecliptic transformation.

See also

References